Human-level control through deep reinforcement learning
Playing Atari with Deep Reinforcement Learning: A Journey into the World of DQN Part 2
This is the second in a series posts where we revisit the landmark papers from DeepMind on Deep Q Learning. In the first post we looked at the 2013 by Mnih et al which introduced the concept of Deep Q Learning and the use of experience replay. In this post we’ll look at the 2015 Nature paper by Mnih et al which introduced a number of improvements to the original algorithm.
The task I’ve set myself is to create an agent that can play the Atari game Breakout and do this:
“Breakout: the agent learns the optimal strategy, which is to first dig a tunnel around the side of the wall, allowing the ball to be sent around the back to destroy a large number of blocks.”
Oh and there’s one last catch - we’re going to do this on a single GPU hosted on Paperspace Gradient in a single session (approximately 6 hours).
To achieve this, we’ll use a Jupyter notebook, an Atari emulator from Gymnasium, and PyTorch. We’ll also log our results to Weights & Biases to track our progress. The complete code is available on GitHub
So my implementation of the 2013 paper gets us an agent who can score on average 16 points against a published score of 168. In 2015 they’d managed to up that to 400 points so we should be able to do better than our first attempt. The human score is 31 points so we’re still a long way off but we’ll get there.
1 Deep Reinforcement Learning
So really there are only a few changes that were introduced in 2015, but boy did they make a big difference. I think the most important is the use of a target network which funnily enough is used to generate the target values for the loss function. This innovation improved training stability and helps to prevent the loss diverging which is caused by the fact the target is “non stationary” which basically means that the parameter update end up changing the target as well as the prediction because the states from which they originate are similar. The idea is that a target network is essentially a copy of the q network that is being trained but it’s weights are kept fixed for a number of steps and are synchronised with the q network periodically. This means that the target values are not changing as often and therefore the loss is more stable.
The other changes are:
- An improved q network architecture. We get an extra conv layer and the kernals have some tweaks.
- It trained on 50 million frames instead of 10 million… Yikes!
- They only make a training iteration every 4 frames instead of every frame.
- They clipped the error term to be between -1 and 1. This sets the loss to the absolute error for terms outside of this range and like mse for terms inside the range. Pytorch has a built in function for this that we can use (smooth_l1_loss). Now confession time - I used this loss function in my first post too because there was no way I could get the model to converge without it.
The complete algorithm for Deep Q-Learning with experience replay is as follows:
Fig 1: DQN with Experience Replay Algorithm from the 2015 Nature paper. Includes the target network.
In code there the differences are pretty small.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
dqn = AtariDQN(DQNDeepmind2015(env.n_actions).to(device), n_actions=env.n_actions).to(device)
target_net = AtariDQN(DQNDeepmind2015(env.n_actions).to(device), n_actions=env.n_actions).to(device)
target_net.load_state_dict(dqn.state_dict())
def get_batch_efficient(self, batch, target_net, collate_fn=None):
s, a, r, s_prime, not_terminated = collate_fn(batch)
y_hat = self(s).gather(1, a.unsqueeze(1)).squeeze() # gather the values at the indices given by the actions a
with torch.no_grad():
next_values, _ = target_net(s_prime).max(dim=1) # IMPORTANT: we're using the target network here
next_values = next_values.clone().detach()
#Bellman equation... our target
y_j = r.detach().clone() + gamma * next_values * not_terminated # if terminated then not_terminated is set to zero (y_j = r)
return y_hat, y_j
Fig 2: Target network used to generate the target values for the loss function
1
2
3
4
5
6
7
8
9
10
11
12
13
14
if len(replay_memory) > replay_start_size and k % replay_period == 0:
optimizer.zero_grad()
batch = replay_memory.sample(bs)
y_hat, y = get_batch_efficient(dqn, batch, target_net=target_net, collate_fn=atari_collate)
loss = loss_fn(y_hat, y)
loss.backward()
torch.nn.utils.clip_grad_value_(dqn.parameters(), max_grad_norm)
optimizer.step()
if k % sync_every_n_steps == 0:
target_net.load_state_dict(dqn.state_dict())
loss = loss.detach()
epoch_loss += loss.item()
Fig 3: Snippet from the training loop showing the target network getting synced with the q network every 10K steps and the training happening every 4 frames (replay_period = 4).
That’s basically it - a few lines of code to change.
2 Preprocessing and Model Architecture
Preprocessing: We use the same preprocessing as in the 2013 paper. The image is converted to greyscale and then resized to 84x84. The image is then cropped to remove the score and the bottom of the screen. The image is then normalized to be between 0 and 1. The last 4 frames are stacked together to form the input to the network.
Model Architecture: The model gets an extra conv layer and we use more kernals otherwise it’s the same as last time around.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class DQNDeepmind2015(nn.Module):
def __init__(self, n_actions):
super(DQNDeepmind2015, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(4, 32, 8, stride=4),
nn.ReLU(),
nn.Conv2d(32, 64, 4, stride=2),
nn.ReLU(),
nn.Conv2d(64, 64, 3, stride=1),
nn.ReLU(),
nn.Flatten(),
nn.Linear(3136, 512),
nn.ReLU(),
nn.Linear(512, n_actions)
)
def forward(self, s):
return self.conv(s)
Fig 4: Pytorch implementation of the 2015 conv net
3 Experiments
The hyperparameters are the same as in the 2013 paper except for:
replay_period = 4 (train on every 4th frame instead of every frame)
As before we ran the experiment on Paperspace Gradient using a machine that has a single GPU with 16GB of memory and a 6 hour timeout. Results are logged to Weights & Biases.
4 Training and Stability
Now at first glance you might look at the loss and think yuck that’s miles worse that the 2013 version, but if we look at the scale it barely eceeds 0.00025 whereas in the first post the loss peaked at 0.3 so it’s actually much better. It also looks like we squeezed out more steps in the environment, but I think that’s probably because we are now only training on every 4th step.
Fig 7: Step Loss
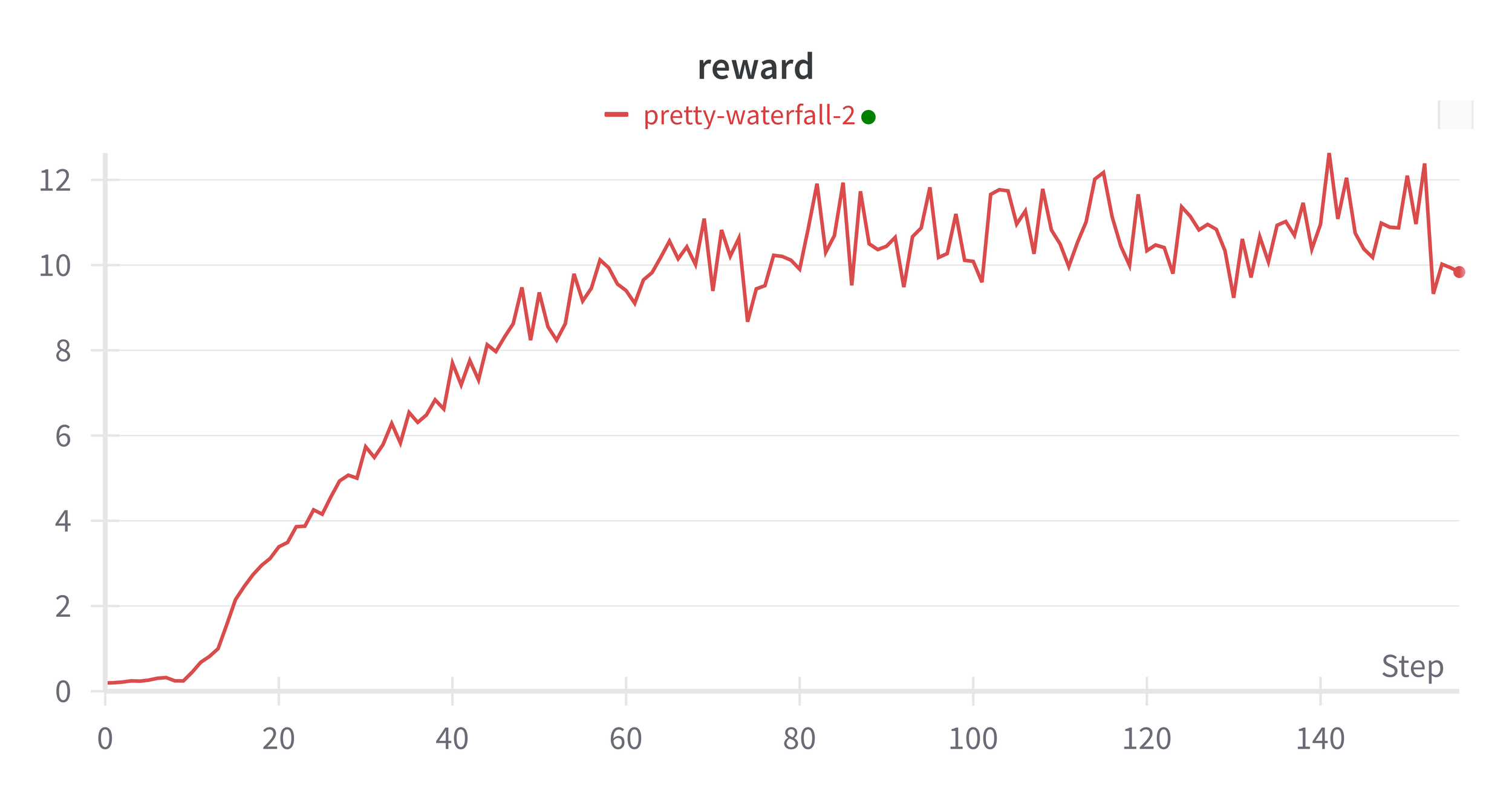
Fig 8: Average Reward per episode during training (rewards are clipped to be between -1 and 1 and episodes are terminated after loss of life)
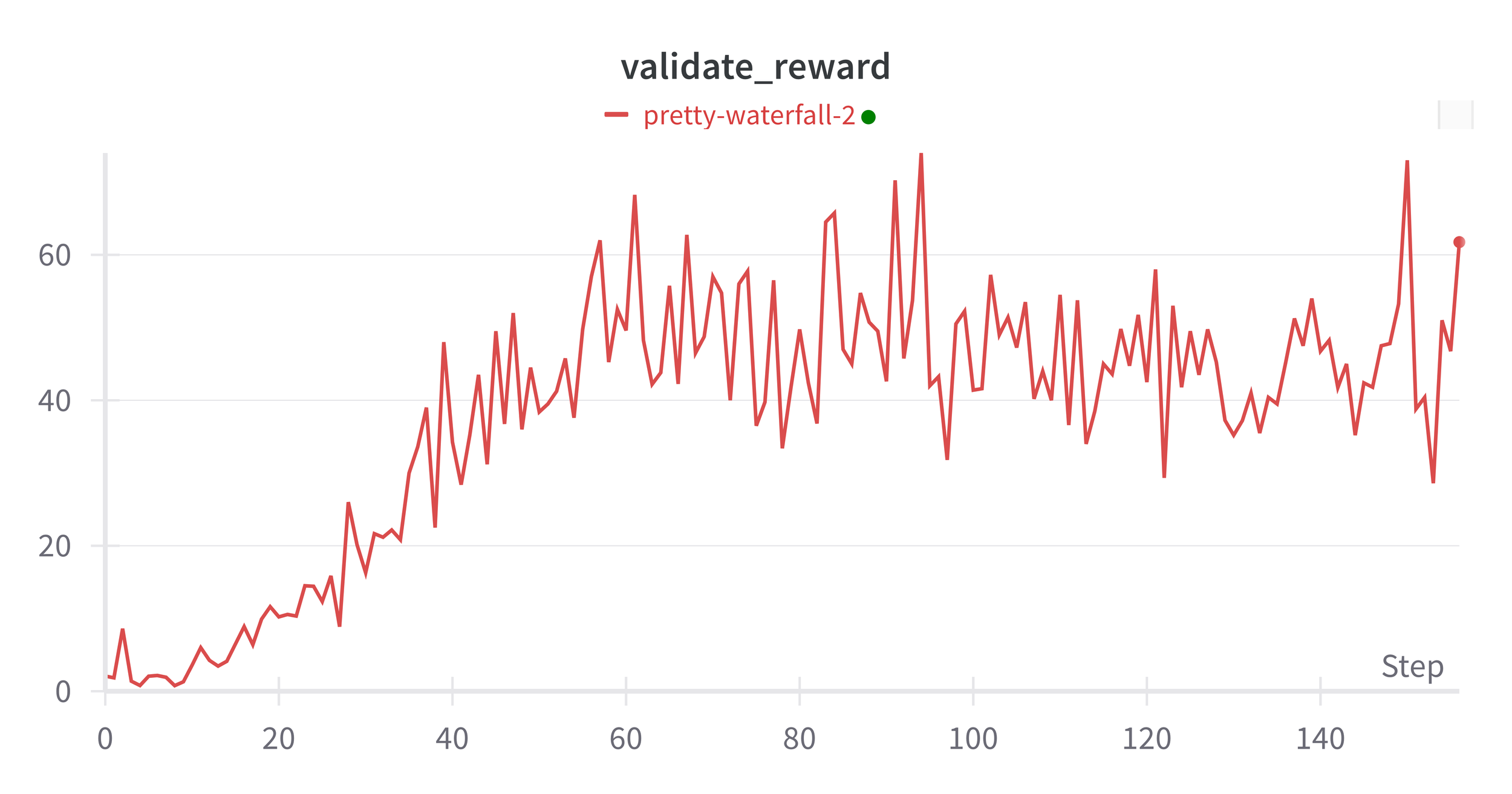
Fig 9: Average Validation Rewards per episode. No clipping of rewards and episodes are not terminated after loss of life.
Improvements start to plateau from around 70 epochs (about 3.5 Million frames), the validation rewards which are an average taken over a 5 minute period get very noisy from around 40 epochs.
5 Main Evaluation
So overall the average rewards during validation end up at 61 which I am pretty happy with. It’s a big improvement on the 16 we had in the first version and is better than the human benchmark, but still a long way off the 400 that Deepmind achieved. In an ideal world we’d up the capacity of the replay memory to the 1M transitions and see how that changes the situation, but we’ll have to leave that for another day.
| Model | Average Score |
|---|---|
| Deepmind 2013 | 168 |
| Deepmind 2015 | 401 |
| Ours 2013 | 16 |
| Ours 2015 | 61 |